【本讲教育信息】

一、教学内容：

1、由立体图形到三视图、由三视图可以说出立体图形的形状。

2、用一个平面截一个几何体，掌握所得截面的形状。

3、掌握平面图形的概念及与三角形的关系。

二、教学目标

1、能够识别一些几何体截面的形状.

2、经历从不同方向看物体的活动，让学生明确物体的三视图及画法，发展学生的空间观念.

3、能正确熟练的画出几何体的视图，能根据几何体的俯视图画出它的主视图、左视图.

4、在具体的情境中认识常见的平面图形。如多边形、扇形，了解平面图形的构成.

三、知识要点分析

1、正确认识用一个平面截一个几何体得到图形的形状

（这是重点）当用一个平面截一个几何体时，平面与几何体的相交位置不同，所得到的平面图形是不一样的，下图是用一个平面去截一个正方体，所有可能得到的图形如下：

2、由立体图形画出三视图

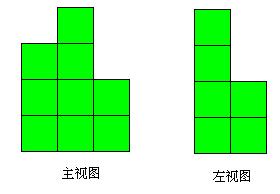
（这是重点）“横看成岭侧成峰，远近高低各不同”这句诗你听到过吗？在数学上我们可以这样理解，当一个几何体放在我们面前，观察几何体的位置不同，所看到的形状也是不同的，从正面看这个几何体称为主视图，从左面看这个几何体称为左视图，从上面看这个几何体称为俯视图，如图所示。

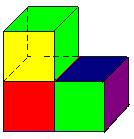
3、由俯视图能画出主视图和左视图

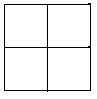
（这是难点）当给出一个几何体的俯视图，根据几何体的特点，能够画出这个几何体的主视图和左视图，解决这类问题首先要了解俯视图中的数据是指看到的是哪个面，所在列中有几层，如图所示，下图是一个几何体的俯视图，你能画出它的主视图和左视图吗.

从上可知，这个几何体高两层，宽有两排，长有三列，所以它的主视图和左视图如下：

主视图 左视图

4、掌握平面图形的相关概念

三角形、四边形、五边形等都是多边形，它们都是由一些不在同一条直线上的线段依次首尾相连组成的封闭图形．

边长与角都分别相等的多边形叫正多边形．

把一个顶点与其余的不相邻的顶点连接起来的线段叫做这个多边形的对角线.

多边形的分割

设一个多边形的边数为n(n≥3) ,从这个n边形的一个顶点出发，分别连接这个顶点与其余各顶点，可以得到________条线段，这些线段又把这个n边形分割成_________个三角形．我们可以通过以下表格进行探索:

多边形	三角形	四边形	五边形	…	n边形
线段数
三角形个数

扇形与弧的定义及区别

(1)弧：圆上两点间的部分叫弧．

(2)扇形：由弧和经过弧的两端的半径所组成的图形叫扇形．

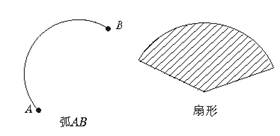
(3)扇形与弧的区别:弧是一段曲线，而扇形是一个面．

【典型例题】

考点一：用平面去截一个几何体

例1：用一个平面去截圆柱，截得的平面图形从形状上来看，可能有哪些结果?请画出这些可能的结果．

【思路分析】当平面与底面垂直相截时得到的平面是一个长方形，当平面与底面平行相截时得到的平面是一个圆，当平面与上底（或下底）面相交并与母线相交得到的截面是一个弓形，当平面倾斜与两条母线相交时得到的是一个椭圆．

解：

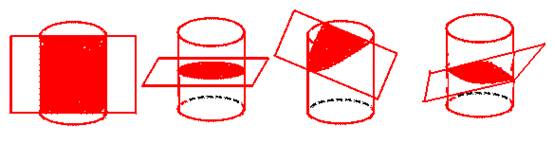
方法与规律总结：在用一个平面去截一个几何体之前应充分想像截面可能的形状，然后与实际操作的结果去对照，反复的练习可以丰富我们的几何直觉和想像力，积累数学活动经验，同时发展我们的空间观念，提高识别简单物体的三视图的能力.

考点二：由立体图形到三视图

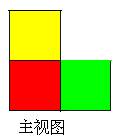
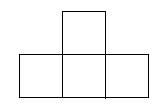
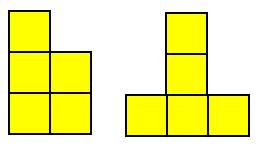
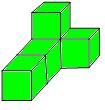
例2：画出图中的五块红色小立方块的搭法的主视图、左视图与俯视图．

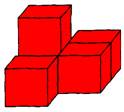
【思路分析】作一几何体的三视图是中考常考的问题，作几何体的三视图关键要清楚，主视图是从哪里看；左视图是从哪里看；俯视图又是从哪里看。只要弄清了这几点，同学们应该不会搞错的。

解：根据题意画图如下：

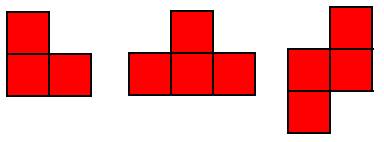
主视图 左视图 俯视图

友情提示: 我们可以知道，在观察同一个物体时，由于所处位置的不同，观察到的图形一般也不相同，所以要抓住其主要特征，关键要分清主视图、左视图、俯视图的异同及其相对性。

例3：如图，桌上放着一摞书和一个茶杯，从左边看到的图形是( )

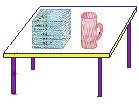
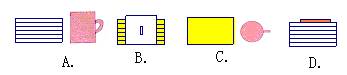
【思路分析】左视图是从这个组合图形的左边来看，一摞书实质上是一个长方体，它的左视图是由几个小长方形组成，茶杯的左视图是一个圆柱，其中一部分被一摞书给遮住，所以看到的图形是D选项。

解：D.

考点三：由三视图到立体图形

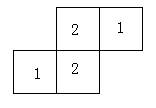
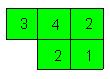
例4：下图是由几个小立方块所搭建的几何体的俯视图，小正方形中的数字表示该位置小立方块的个数。请画出这个几何体的主视图和左视图．

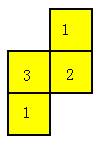
【思路分析】从俯视图上可以看出，这个由小立方体搭建的几何体，有三层高，三列宽，从正面看是由两排组成，根据上面的分析可以画出几何体的主视图和左视图.

解：图形如下：

主视图 左视图

友情提示：解决这类问题的关键是要找出这个几何体有几层高，有几列宽，有几排长组成。

例5：在一仓库里堆放着若干个相同的正方体货箱，仓库管理员将这堆货箱的三视图画了出来．如图所示，则这堆正方体货箱共有（ ）

A．9箱 B．10箱 C．11箱 D．12箱

【思路分析】根据俯视图确定小正方体块的位置分布；根据左视图与主视图确定某个位置小正方体块的个数。小正方体的具体分布情况如下图所示：

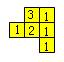
解:A.

方法与规律总结:熟练掌握左视图和主视图，确定出俯视图每个位置上有几个小正方体，然后再确定有几个小正方体。

考点四：平面图形的初步认识

例6：一个五边形切一刀后变成（ ）.

A.五边形

B.六边形

C.六边形或五边形

D.三角形或四边形或五边形或六边形.

【思路分析】如下图,一个五边形切一切后(切去阴影部分)有四种情况:

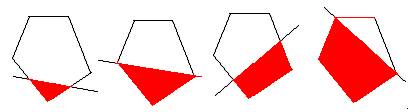
解：D

【本讲涉及的数学思想和方法】

本讲主要讲述用一个平面去截一个几何体，截出的面叫做截面，它的形状随截法而改变．我们从不同的方向观察同一个物体时，可能看到不同的图形，把从正面看到的图叫做主视图，从左面看到的图叫做左视图，从上面看到的图叫做俯视图，在面与体的转换中丰富几何直觉和数学活动经验，发展空间观念．

预习导学案（2）

(有理数的有关概念）

一、预习前知

1、什么是负数？什么是有理数?

2、什么是数轴？什么是相反数？什么是绝对值?

3、怎样用数轴和绝对值来比较两个有理数的大小?

二、预习导学

探究与反思

探究任务1：为什么引入负数

在负数没有出现时,人们是怎样表示与正数有相反意义的数的?

【反思】（1）负数引入的必要性

（2）负数出现后,有理数的分类是什么?

探究任务2：数轴在表示数上有什么作用? 绝对值所表示的意义是什么？

1、找出数轴的三要素及数轴与有理数的关系.

2、绝对值所表示的意义与小学中学习的距离有什么关系?

【反思】（1）一个正数的绝对值是什么？一个负数的绝对值是什么？

（2）0的绝对值有几种说法？

三、牛刀小试

1. 如果收入30元,表示为+30,那么支出30,表示为________.

2. 下列说法正确的是（ ）

A. 有理数中有最大的数,没有最小的数

B. 有理数中有最小的数,没有最大的数

C. 0既不是负数,也不是正数

D. -1是最大的负数

3. │4│=______。

4. ________的绝对值等于它本身。

5. 若，则x=________．

【模拟试题】(答题时间:60分钟,满分100分)

一、选择题(每小题4分,共40分)

1. 用一个平面去截球得到的图形是( )

A.长方形 B.正方形 C.梯形 D.圆

2. 下列说法正确的是( ）

A. 用一个平面去截正方体能得到八边形 B.用一个平面去截长方体能得到八边形

C. 用一个平面去截圆柱能得到梯形 D.用一个平面去截圆台能得到梯形

3. 一个几何体的三视图如图所示，这个几何体是（ ）

A．棱柱 B．圆柱 C．圆锥 D．球

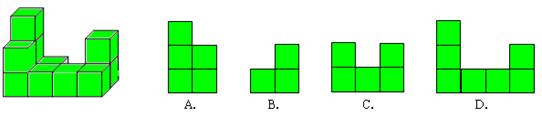
﹡4. 如图是由相同小正方体组成的立体图形，它的左视图为（ ）

﹡5. 下列有关三棱柱的截面说法正确的是( )

A.不可能是长方形 B.不可能是三角形 C.不可能是正方形 D.可能是长方形或三角形

﹡6. 如图所示的圆锥的三视图是( )

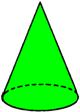
A．三个三角形

B．主视图和侧视图都是三角形，俯视图是三角形和三角形内的一个点

C．主视图和侧视图都是三角形，俯视图是圆

D．主视图和侧视图都是三角形，俯视图是圆和圆心

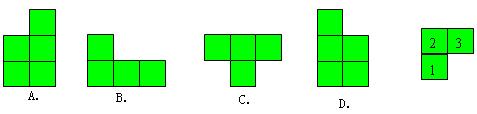
﹡7. 下图是由几个小立方块搭成的几何体的俯视图，小正方形中的数字表示在该位置的小立方块的个数，那么这个几何体的主视图是（ ）

﹡8. 如图,是一个由若干个相同的小正方体组成的几何体的三视图,则组成这个几何体的小正方体的个数是( )

A.7个 B.8个 C.9个 D.10个

﹡9、如图是由若干个同样大小的立方体搭成的几何体的俯视图，小正方形中的数字表示该位置立方体的个数，则这个几何体的主视图是（ ）

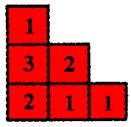
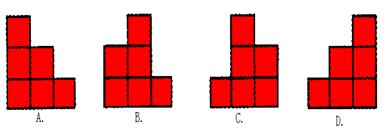
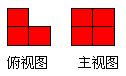
﹡﹡10、一个几何体是由一些大小相同的小正方块摆成的，其俯视图与主视图如图所示，则组成这个几何体的小正方块最多有（ ）

A．4个 B．5个 C．6个 D．7个

二、填空题（每题4分，共24分）

11. 十边形有_________条边.

﹡12. 七棱柱有_____个面,用一个平面截七棱柱能不能得到七边形_____（填“能”或“不能”）。

13. 从一个多边形的某个顶点出发,分别与其余各顶点连接,把此多边形分割成10个三角形,则原多边形是_______边形.

14. 三种视图都是正方形的几何体是我们学的_______.

﹡15如图是由四个相同的小立方体组成的立体图形的主视图和左视图，那么原立体图形可能是 ．（把下图中正确的立体图形的序号都填在横线上）

﹡﹡16、如图所示是某种型号的正六角螺母毛坯的三视图，则它的侧面积为 ．

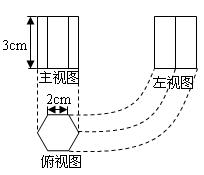
三、解答题（共36分）

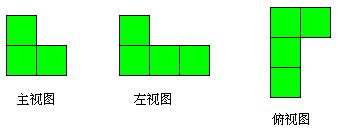
﹡17、（本题9分）画出下列几何体的三视图.

﹡18、（本题7分）一个四棱柱被一刀切去一部分，试举例说明剩下的部分是否可能还是四棱柱.

﹡19、（本题8分）请利用若干个三角形拼出一个你喜欢的图案,并说明你的创意.

﹡﹡20. （本题12分）如图所示是由几个小正方体组成的几何体的俯视图，小正方形中的数字表示在该位置的小正方体的个数，请画出这个几何体的主视图和左视图.

【试题答案】

一、

1、D【思路分析】用一个平面去截球得到的图形只有圆.

2、D【思路分析】用一个平面去截一个正方体和长方体不可能得到八边形,用一个平面去截一个圆柱得到的是长方形和圆,不会是梯形,所以答案为D.

3、B【思路分析】俯视图是圆的有圆柱和球两种,再联系主视图和左视图只能是圆柱了.

4、A【思路分析】从正面能看到下面一层是两个面,第二层是两个面,第三层的左边是一个面.所以答案为A.

5、D【思路分析】用一平面去截三棱柱所得的截面可能是长方形,也可能是正方形,还可能是三角形.

6、D【思路分析】圆锥的主视图和侧视图都是三角形，俯视图是圆和圆心.

7、A【思路分析】由俯视图可知,最里面一列的左边共2个小正方块,右边是3个小正方块,外面一列左边是一个正方块,所以它的主视图是A。

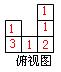
8、C【思路分析】根据题目提供的主视图和左视图,可以确定俯视图中每个位置对应的小正方体的个数,如下图,可知有9个小正方体.

9、A【思路分析】从俯视图的个数来看主视图的左边是3层，中间是2层，右边是1层，所以选A.

10、C【思路分析】由主视图可以得到最下面一层最多有四个小正方块,上面一层最多有两个小正方块,所以这个几何体最多有6个小正方块.

二、

11、10 【思路分析】根据平面图形的定义可知十边形有10条边。

12、9 能 【思路分析】七棱柱的底面是七边形,有七个侧面,共有9个面,用一平面过每一条侧棱,这样得到的平面是七边形.

13、12 【思路分析】从四边形的一个顶点出发,可以把四边形分成两个三角形;从五边形的一个顶点出发可以把五边形分割成三个三角形;从六边形的一个顶点出发, 可以把六边形分成四个三角形,依次类推,可以判断从一个多边形的顶点出发,把多边形分成10个三角形,则此多边形是10+2=12边形.

14、正方体。

15、①②④【思路分析】根据从正面和左面看到的图形，可知①②④都符合要求.

16、36【思路分析】6×2×3=36.

三、

17、【思路分析】根据主视图、左视图和俯视图的观察方位，正确地找出所看到的面的位置，画出图形。

解：

18、【思路分析】这是一道很简单但也很典型的“截几何体”的试题.注意多方面考虑即可正确解答.

解：可能，只要沿着平行于棱柱的侧面或底面的平面切即可，其它方法不行.

19、【思路分析】设计出的图案必须是由三角形构成的,创意涉及的内容比较广泛,可以是环保、和平等方面的内容.

解：图案如下,创意:我们爱和平 (答案不唯一).

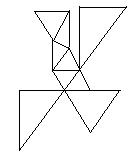
20、【思路分析】确定每一列上最多有几个面，这样能够准确地画出几何体的主视图和左视图。