【本讲教育信息】

一、教学内容：

集合的概念与基本运算

二、学习目标：

1、通过实例了解集合的含义，体会元素与集合的“属于”关系，掌握某些数集的专用符号；

2、理解集合的表示法，用集合语言对事物进行准确的分类，能选择自然语言、图形语言、集合语言（列举法或描述法）描述不同的具体问题，感受集合语言表示数学内容的简洁性和准确性；

3、理解集合之间包含与相等的含义，能识别给定集合的子集。培养分析、比较、归纳的逻辑思维能力；

4、能在具体情境中，了解全集与空集的含义；

5、理解两个集合的并集与交集的含义，会求两个简单集合的交集与并集；培养从具体到抽象的思维方法；

6、理解在给定集合中，一个子集的补集的含义，会求给定子集的补集；

7、能使用Venn 图表达集合的关系及运算，体会直观图示对理解抽象概念的作用。

三、知识要点

（一）集合的含义与表示

1、集合

（1）一般地，指定的某些对象的全体称为集合；

（2）集合常用大写字母A、B、M、N……标记；

（3）一些常用的数集及其记法：

自然数集：N；

正整数集：N₊；

整数集：Z；

有理数集：Q；

实数集：R；

2、元素

（1）集合中的每个对象叫作这个集合的元素；

（2）元素常用小写字母a,b,c,d,……标记；

3、元素与集合的关系：

若a在集合A中，就说a属于集合A，记作a∈A；若a不在集合A中，就说a不属于集合A，记作aA。

4、集合的表示方法

（1）列举法：把集合中的元素一一列举出来写在大括号内。如：小于10的所有质数组成的集合用列举法可以表示为

A＝｛2，3，5，7｝。

（2）描述法：描述该集合中所有元素都应该满足的条件的方法。如：大于1而小于10的所有实数组成的集合用描述法可以表示为

B＝｛x｜1<x<10｝。

（3）图示法：用一个封闭的曲线的内部直观地表示一个集合的方法，这个封闭的曲线称为Venn图。如：小于10的所有质数组成的集合用Venn图可以表示为

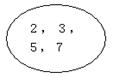
5、集合的分类

（1）有限集：含有有限个元素的集合；

（2）无限集：含有无限个元素的集合；

（3）空集：不含任何元素的集合，用符号φ表示。

例1 下列不能形成集合的是（ ）

A、你现在的家庭成员； B、本单位已退休人员；

C、老年人； D、本班的学生

分析：因为集合一旦形成，那么对任何一个对象而言，它要么属于这个集合，要么不属于这个集合。但是，如何判断一个人是不是老年人尚无统一标准，所以不能形成集合。

答：C。

（二）集合的基本关系（本课学习的重点）

1、包含

（1）一般地，对于两个集合A与B，如果集合A中的任何一个元素都是集合B的元素，即若a∈A，则a∈B，就说集合A包含于集合B，或集合B包含集合A。记作

AB（或BA）。

这时我们就说集合A是集合B的子集。

任何一个集合是它本身的子集，即AA。

2、相等：对于两个集合A与B，如果集合A中的任何一个元素都是集合B中的元素，同时集合B中的任何一个元素都是集合A中的元素，这时我们就说集合A与集合B相等，记作

A＝B。即若AB，且BA，则A＝B。

3、真子集

（1）对于两个集合A与B，如果AB且A≠B，我们就说集合A是集合B的真子集，记作

AB（或BA）

（2）空集是任何集合的子集，即对任意集合A，都有：φA；空集是任何非空集合的真子集，即若集合A≠φ，则有φA。

例2 试写出集合A={1，2，3，4，5}的所有子集。

分析：以子集所含元素的个数分别为0，1，2，3，4，5进行分类

解答：共有32个：φ，{1}，{2}，{3}，{4}，{5}，{1，2}，{1，3}，{1，4}，{1，5}，{2，3}，{2，4}，{2，5}，{3，4}，{3，5}，{4，5}，{3，4，5}，{2，4，5}，{2，3，5}，{2，3，4}，{1，4，5}，{1，3，5}，{1，3，4}，{1，2，5}，{1，2，4}，{1，2，3}，{1，2，3，4}，{1，2，3，5}，{1，2，4，5}，{1，3，4，5}，{2，3，4，5}，{1，2，3，4，5}。

思考：若已知集合A有n个元素，则集合A的子集有多少个？真子集有多少个？

（三）集合的基本运算（本课学习的重点和难点）

1、交集：一般地，由既属于集合A又属于集合B的所有元素组成的集合，叫作A与B的交集，记作A∩B，读作“A交B”，即

A∩B＝｛x|x∈A且x∈B｝。

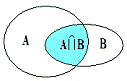
2、并集：一般地，由属于集合A或属于集合B的所有元素组成的集合，叫作A与B的并集，记作A∪B，读作“A并B”，即

A∪B＝｛x|x∈A或x∈B｝。

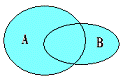
例3 已知集合A={x|0<x<3},B={x|－1≤x≤2}，求A∩B、A∪B。

分析：集合A和B都是数集，可借助数轴进行研究。

解：在数轴上分别表示出集合A与集合B，如图：

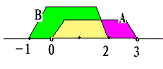
则得：A∩B={x|0<x≤2}， A∪B={x|－1≤x<3}。

3、全集：一般地，在研究某些集合的时候，这些集合往往是某个给定的集合的子集，这个给定的集合叫作全集，常用符号U表示。全集含有我们所要研究的这些集合的全部元素。

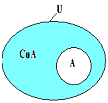
4、补集（或余集）：设U是全集，A是U的一个子集（即AU），则由U中所有不属于A的元素组成的集合，叫作U中子集A的补集（或余集），记作：C_UA，即

C_UA={x|x∈U，且xA}。

5、求集合的交集、并集和补集都是集合的运算； 两个集合运算的结果仍然是一个集合。

②主要运算性质：

A∩A=A，A∪A=A；

A∩B=B∩A，A∪B=B∪A；

（A∩B）∩C=A∩（B∩C），（A∪B）∪C=A∪（B∪C）；

A∩（B∪C）=（A∩B）∪（B∩C），A∪（B∩C）=（A∪B）∩（A∪C）；

C_U（A∩B）=C_UA∪C_UB，C_U（A∪B）=C_UA∩C_UB

③主要运算关系：

A∩BA，A∩BB；A∪BA，A∪BB；

A∩B=AAB，A∪B=AAB；

说明：对以上运算法则和运算关系的理解可结合Venn图进行。

例4 已知集合A={x|0≤x<1}，求C_RA.

分析：本题求解集合A在实数集R中的补集，即求所有不属于A的元素组成的集合。

解：C_RA={x|x<0或x≥1}.

【典型例题】

考点一：集合的含义

对集合含义的考查主要集中在对集合中元素的无序性、互异性和确定性的考查上，常见错误是在解题中忽略了集合中元素必须具备的这三种性质。

例5 已知集合A={1，3，a²}，B={a+2}，若BA，求实数a。

解：由BA可得a+2=1或a+2=3或a+2=a²，从而解得a=－1或a=1或a=2。又当a=－1或a=1时，a²=1，即集合A中元素不满足互异性，故a=2。

说明：本题解答中的常见错误是没有对集合A中元素的互异性进行检验，从而得到a=－1或a=1或a=2。

考点二：空集的性质

空集是任何集合的子集，是任何非空集合的真子集。这是空集的重要性质，在利用两个集合之间的关系求解参数的时候容易遗漏。

例6 已知集合A={x|（x－1）（x－a）<0}，B={x|1<x<2}，AB，求实数a的范围。

解：讨论：

当a<1时：A={x|a<x<1}，A∩B＝φ，不合题意；

当a>1时：A={x|1<x<a}，由AB，a≤2；

当a=1时：A=φ，亦满足题意。

综上所述：1≤a≤2。

说明：a=1时，A=φ，由空集的性质知：此时AB。此解极易被忽略。

考点三：判断两个集合之间的关系

对两个集合之间关系的研究主要看元素所满足的条件（或性质），寻找其间的异同点。

例7 已知集合A={x|x=4k±1,k∈Z}，B={x|x=2k+1,K∈Z}，试判断集合A、B的关系。

解：对集合A，元素x=4k±1=2k+（2k±1），即集合A中的元素可以表示为一个奇数和一个偶数之和，仍是一个奇数，故集合A是全体奇数形成的集合，所以A=B。

说明：本题也可对k分奇数和偶数进行讨论。解答这种题型的常见问题有二，一是取特殊值试解，然后归纳；二是不知如何下手，此时需要对两个集合中元素所满足的条件式进行变形，尽量使得两者在形式上更为接近，再分析其间的差异，如本题就可将A中元素改写为x=4k±1=2k+（2k±1），即一奇数与一偶数之和，B中元素改写为x=2k+1=k+（k+1），也是一奇数和一偶数之和，故可得出结论。

考点四：利用两个集合之间的关系求参数

利用两个集合之间的关系进行解题是一个重点题型，考查十分频繁。

例 参见考点一和考点二的例题。

考点五：集合运算

直接求集合间的运算也是一个重点题型，大多结合解简单的不等式进行考查。

例8 已知集合M={x|x<3}，N={x|log₂x>1}，则M∩N等于（ ）

A、φ B、{x|0<x<3} C、{x|1<x<3} D、{x|2<x<3}

解：D。

说明：这是2006年全国卷二的第一题，需先解一个十分简单的对数不等式log₂x>1。

四、本课涉及的主要数学思想方法

1、分类讨论的思想：在利用两个集合间的关系进行解题时，往往要进行分类讨论，如对条件“AB”往往就要分“A=φ”和“A≠φ”两种情形进行讨论；通过此类题型的训练，可以促进同学们思维严密性的提高。

2、数形结合的思想：研究两个集合间的关系和运算时，可以借助Venn图、数轴等几何图形进行研究或帮助理解。通过此类题型的训练，可以使同学们快速把握数学概念、数学关系的几何特征，从而快速求解。

【模拟试题】（答题时间：50分钟）

一、选择题

1、设集合M={x|x²－x<0}，N={x||x|<2}，则（ ）

A、M∩N=φ B、M∩N=M C、M∪N=M D、M∪N=R

2、下列集合中，表示空集的是（ ）

A、{x|x+3=3} B、{x|x²－x+1=0，x∈R}

C、{y|y²>0,y∈R} D、{（x,y）|y²=－x²，x,y∈R}

3、若A={x|x²=1},B={x|x²－2x－3=0}，则A∩B＝（ ）

A、{3} B、{1} C、φ D、{－1}

4、设a,b∈R，集合{1，a+b,a}={0,,b},则b－a=（ ）

A、1 B、－1 C、2 D、－2

5、如果U={x|x是小于9的正整数}，A={1，2，3，4}，B={3，4，5，6}，那么C_UA∩C_UB=（ ）

A、{1，2} B、{3，4} C、{5，6} D、{7，8}

6、若A、B、C为三个集合，A∪B=B∩C，则一定有（ ）

A、AC B、CA C、A≠C D、A=φ

7、定义集合运算：A※B={z|z=xy（x+y）,x∈A,y∈B}.设集合A={0，1}，B={2，3}，则集合A※B的所有元素之和为（ ）

A、0 B、6 C、12 D、18

二、填空题

8、已知集合A={x∈R|ax²+2x+1=0,a∈R}只有一个元素，则a的值为 ；

9、满足{1，3}∪A={0，1，2，3}的所有集合A的个数是 。

三、解答题

10、已知集合A={a－2,2a²+5a,12}且－3∈A，求a的值。

11、已知全集为R，A={y|y=x²－2x－2},B={y|y=－x²－2x+2}，求（C_RA）∪B.

12、已知集合A={x|x²+2x+m=0}，B={x|x²－3x+2=0}，A∩B≠φ，求m的取值范围。

13、已知集合A={x|ax²+2x+1=0,a∈R,x∈R}.若A中至多只有一个元素，求a的取值范围。

【试题答案】

一、选择题：1、B 2、B 3、D 4、C 5、D 6、A 7、D

二、填空题

8、0或1；

9、4；

三、解答题

10、解：由题知，a－2=－3或2a²+5a=－3。

若a－2=－3，则a=－1；又当a=－1时：2a²+5a=－3，故a=－1应舍去；

若2a²+5a=－3，解得a=－1（舍）或a=－.

综上所述：a=－.

11、解：y=x²－2x－2=（x－1）²－3≥－3，故C_RA={y|y<－3}；B={y|y=－x²－2x+2}={y|y=－（x+1）²+3}={y|y≤3}，故（C_RA）∪B={y|y≤3}；

12、解：可解得集合B={1，2}，由A∩B≠φ，可分别解得m=－3或m=－8。

13、解：讨论：Ⅰ、若A中恰有一个元素，可解得a=0或1；

14、Ⅱ、若A中无元素，可解得a>1；

综上所述可知：a=0或a≥1。