【本讲教育信息】
一. 教学内容：
22.3 二次根式的加减法
二. 重点、难点：
1. 重点：
（1）了解同类二次根式的概念，掌握二次根式的加减运算；
（2）能进行二次根式的混合运算.
2. 难点：
（1）能结合乘法公式和因式分解的方法进行二次根式的混合运算.
（2）能够运用二次根式的混合运算解决一些简单的实际问题.
三. 知识梳理：
1. 同类二次根式
几个二次根式经过化简之后，如果被开方数相同，那么这几个二次根式就叫做同类二次根式。如
，
，所以
和
是同类二次根式。
说明：
（1）判断同类二次根式的方法：
①首先将不是最简形式的二次根式化为最简二次根式；
②再看被开方数是否相同。
（2）几个二次根式是否是同类二次根式，只与被开方数及根指数有关，而与根号外的因式无关。
合并同类二次根式与合并同类项类似，理论依据都是逆用乘法对加法的分配律，合并同类二次根式，只是把它们的系数相加，根指数和被开方数都不变。
2. 二次根式的加减法
二次根式的加减实质上就是合并同类二次根式，它与合并同类项类似。如4
+3－5=（4+3－5）。必须注意不是同类二次根式的不能合并，如+
≠
。
二次根式的加减一般可以分三步进行：
①将每一个二次根式化成最简二次根式；
②找出其中的同类二次根式；
③合并同类二次根式。
需要注意的是：
①进行二次根式的加减运算时，过去在学习整式的加减运算中的交换律，结合律及去括号，添括号法则仍然适用；
②二次根式的加减运算结果应写成最简结果或几个非同类二次根式的和。
3. 二次根式的混合运算
（1）二次根式的混合运算与整式的混合运算类似。其运算顺序是：先乘方开方，再乘除，最后加减，有括号的先算括号里面的（或先去括号再计算）。
（2）在二次根式混合运算的过程中，每个二次根式可以看做一个“单项式”，几个被开方数不同的二次根式的和可以看做“多项式”，故二次根式的运算可以看做整式的运算。
（3）实数运算中的运算律，运算法则及乘法公式在二次根式的运算中仍然适用。
【典型例题】
例1. 把下列各式化成最简二次根式：
（1）
； （2）
； （3）
；
（4）
； （5）
。
分析：化简二次根式的一般步骤：
（1）把被开方数（式）分解质因数（式），化为积的形式；
（2）把根号内能开得尽方的因数（或式）移到根号外；
（3）化去根号内的分母.有带分数要化成假分数，有小数化成分数。
解：
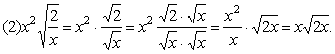
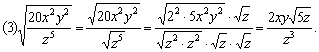
（5）
例2. 下列二次根式中，哪些是同类二次根式?
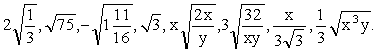
分析：先化二次根式为最简二次根式.最简二次根式只要被开方数相同，就是同类二次根式，与根号外面的因式无关。
解：
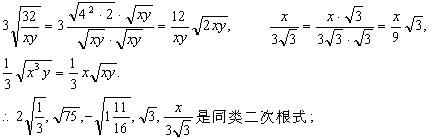
例3. 已知最简根式
、
是同类根式，求代数式
的值。
分析：同类根式必须同时满足以下条件：①为最简根式；②根指数相同；③被开方数相同。同类二次根式概念为本题提供了求出
、
的条件，从而最终求出代数式的值。
解：因为最简根式、是同类根式，
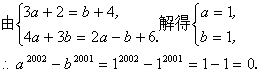
例4. 计算：
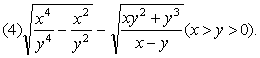
分析：先化简二次根式，再合并同类二次根式。
解：
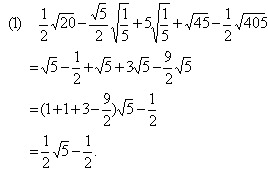
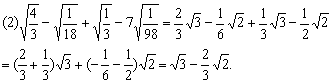
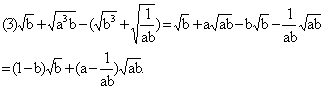
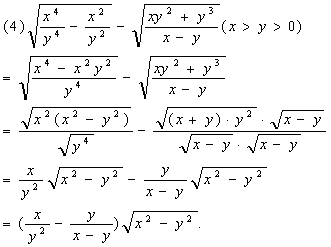
例5. 计算：
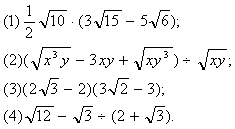
分析：这里可以把二次根式看成是一个“单项式”或者“多项式”利用整式乘法或除法法则进行运算。第（1）、（2）、（3）题都与整式运算类似。第（4）题，因为除法不满足分配律，可先转化成分数形式，再分母有理化。
解：
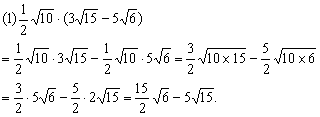
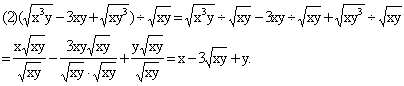
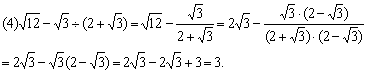
例6. 计算：
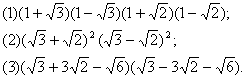
分析：原来学过的所有运算律、运算法则及乘法公式仍然适用二次根式的运算.这三道题都可以利用平方差公式或完全平方公式。
解：（1）
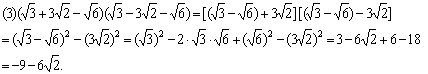
例7. 已知
，
，求
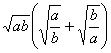的值。
分析：直接代入求值比较麻烦，可考虑把代数式化简再求值，并且、的值的分母是两个根式，且互为有理化因式，故
必然简洁且不含根式，
的值也可以求出来。
解：由已知得：＝
＝
，
；
∴原式＝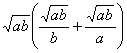
＝＝.
例8. 计算：
分析：一般地，两个含有二次根式的代数式相乘时，如果它们的积不含二次根式，我们就说这两个代数式互为有理化因式。解决此题首先要化去分母中的根号，则关键是选择一个适当的数（或代数式），用这个数（或代数式）去乘分式的分子和分母，从而使分母不含根号，即分母有理化。
解：
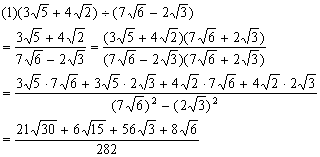
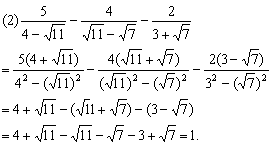
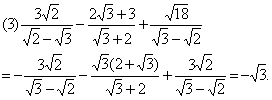
例9.
已知x，y都是正整数，且 
，求 
的值.
分析：因为只有同类二次根式才能合并，而
=
，所以易知
、
与是同类二次根式，于是可求出x，y的值。
解：∵=
∴设=
，=
，（
、为正整数）
则有+= ，即+=3；
∵、为正整数， =1，=2或=2，=1，
∴
=222，
=888或=888，=222
∴+=1110.
例10. 有一艘船在点O处测得一小岛上的电视塔A在北偏西60°的方向上，船向西航行20海里到达B处，测得电视塔在船的西北方向。问再向西航行多少海里，船离电视塔最近？（结果保留根号）
分析：此题将二次根式与解直角三角形相结合，先解直角三角形，再根据二次根式的有关性质进行化简.船离电视塔最近时，应为线段AC的长。
解：设BC=，则在R
△ACB中，∠ABC=45°，所以AC=BC=
在R△ACO中，∠AOC=30°，AC=（+20）÷，
所以有：（+20）÷=，
解得：=
即==
=
+10
答：再向西航行（+10）海里，船离电视塔最近。
【模拟试题】（答题时间：40分钟）
一、选择题
1. 下列根式中，最简二次根式是 （ ）
A. 
B.
C.
D.
2. 与
不是同类二次根式的是 （ ）
A. 
B.
C.
D.
3. 下列根式中，是同类二次根式的是 （ ）
A. 
和
B.
和
C. 
和
D.
和
4. 下列计算中，错误的是（ ）
A. 
B. 
C. 
D. 
5. 化简
的结果是（ ）
A. 0 B.
－ C.
D.
6. 下列计算中，正确的是 （ ）
A. 
B.
C.
D.
7. 若m<0，则把式子
根号外面的因式移到根号里的式子应是 （ ）
A. 
B.
C. 
D.
8. 计算
的结果是（ ）
A. 
B.
C.
1 D.
－1
9. 已知a=
，b=
，则a与b的关系是 （ ）
A. a=b B.
a+b=
10. 下列计算正确的是（ ）
A. 
B. 
；
C. 
D. 
二、填空题
11. 化简
=________；
=____________（x>0，y>0）。
12. 若
与
是同类二次根式，则b=______。
13. 若最简二次根式
和
是同类二次根式，则x=________。
14. 在二次根式
中，________________是同类二次根式。
15. 若最简根式
和
是同类根式，则m=______，n=_______。
16. 
=__________，
=__________。
17. 若x=
，则x2－x+1=________。
18.
化简
=____________。
三、解答题
19. 计算或化简：
（1）
（2）
（3）
（4）
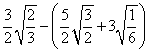
（5）
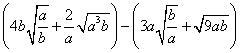
（6）
20. 已知x=
，求
的值。
【试题答案】
一、选择题
1. B 2.
C 3.
C 4.
D 5.
B
6. C 7.
A 8.
A 9.
A 10.
D
二、填空题
11.
；
12. 
；
13. ；
14. 
，
；
15. 2，3；
16. 
；
17. 
；
18.
.
三、解答题：
19. （1）
（2）3 （3）1
（4）
（5）0 （6）－2
20. 2－