【本讲教育信息】
一. 教学内容：
1、理解轴对称图形与轴对称的意义，并能说出它们的区别
2、学习简单的轴对称图形——角、线段，以及角平分线、垂直平分线的意义和性质。
3、能应用角平分线和中垂线的性质进行有关的计算或证明。
二. 学习重难点：
轴对称和轴对称图形，角平分线以及中垂线的概念、性质与应用是本讲的重点，轴对称和轴对称图形的异同，中垂线和角平分线的性质的应用是本讲的难点。
三. 知识要点讲解：
1、 请同学们欣赏下列图片，美吗？漂亮吗？
思考：五角星沿着某条直线对折，直线两旁的部分重合吗？
2、轴对称图形：
如果一个图形沿一条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形。这条直线叫做对称轴。
注：①、轴对称图形是一个图形，
②、两旁的部分重合——即：两旁的部分全等
思考：你还能举出其他的例子吗？
英语字母中的轴对称图形，汉字中的轴对称图形等。
▲、直线两侧的这两个双喜字有什么关系？
3、两个图形的轴对称性：
对于两个图形，如果沿着一条直线对折后，它们能够完全重合，那么称这两个图形关于这条直线成轴对称，这条直线就是对称轴。
例1、下列图形是轴对称图形吗？如果是轴对称图形，画出它的一条对称轴。
考一考：
答案：_________
4、简单的轴对称图形：
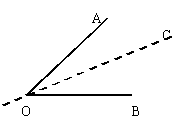
⑴、想一想，角是轴对称图形吗？
如果是，它的对称轴是什么？请看：
角是轴对称图形，有一条对称轴，它的对称轴是：
角平分线所在的直线
思考：在角AOB的平分线OC上任取一点P，则点P
到角的两边的距离有什么关系？
分析：△POM与△PON全等吗？你是如何判定的？
∵∠POM=∠PON，∠PMO=∠PNO=90°，OP=OP
∴△POM≌△PON（AAS）
∴ PM=PN（全等三角形的对应边相等）
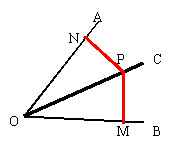
结论：角平分线上的点到角的两边的距离相等。
思考：在上面的问题中，除了线段PM=PN外，还能得到什么结论？
推理：∵点P在OC上，（OC是∠AOB的平分线）， PM⊥OB、PN⊥OA ∴ PM=PN
角平分线上的点到角的两边的距离相等
⑵、线段是轴对称图形吗？它有几条对称轴？你能画出来吗？
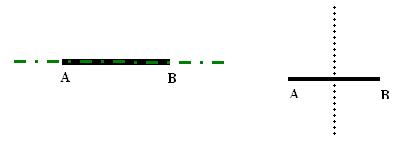
⑶、线段的中垂线：平分线段且垂直于线段的直线叫做线段的垂直平分线，又叫中垂线。
注意：线段有两条对称轴，一条是：线段所在的直线，
另一条是：线段的中垂线。
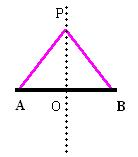
问题：在线段AB的中垂线上任取一点P，则：PA与PB有何关系？你能说明理由吗？
理由：∵ PA⊥AB ∴∠POA=∠POB=90°
又∵ AO=OB，PO=PO （SAS）
∴ △POA≌△POB
∴ PA=PB （全等三角形的对应边相等）
推理：∵ PO是线段AB的中垂线 ∴ PA=PB
⑷、角平分线的性质与中垂线的性质的区别：
角平分线的性质： 点——到——线 的距离 （有垂直条件）
中垂线的性质： 点——到——点 的距离
【典型例题】
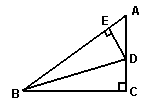
例2、在Rt△ABC中，BD是角平分线，DE⊥AB，垂足为E，DE与DC相等吗？为什么？
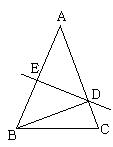
例3、（1） 如图， AB是△ABC的一条边，DE是AB的垂直平分线，垂足为E，并交BC于点D，已知AB=
.
解：
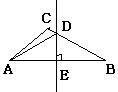
（2）如图，在△ABC中，AB=AC=
解：
例4、已知，在Rt△ABC中，∠C=
，AD平分∠BAC交BC于D，若BC=32，且BD：CD=9：7，则D到AB的距离为：
A.
18 B.
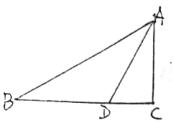
解：
例5、（1）在△ABC内找一点P，使得点P到△ABC的三条边的距离相等。
分析：点P到△ABC的三边AB、AC、BC的距离相等，是点到直线的距离相等，所以，点P应在三角形的三个内角平分线上，所以作出两个角的平分线即可。
（2）在平面内找一点P，使得点P到ABC三点的距离相等即：PA=PB=PC
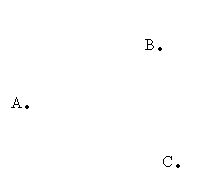
分析：点P到三个点A、B、C的距离相等，是点到点的距离相等，所以，点P在线段AB、AC、BC的中垂线上，所以，只要作出三条线段的中垂线即可。
课堂小结：
本节课我们主要学习了轴对称图形、轴对称的意义以及两个基本的轴对称图形——线段和角，研究了它的性质，即：中垂线和角平分线的性质，理解它们的区别与联系。
角平分线的性质： 点——到——线 的距离 （有垂直条件）
中垂线的性质： 点——到——点 的距离
【模拟试题】（答题时间：70分钟）
一、填空题
1、线段是轴对称图形，它的对称轴是_________________________。
2、角是轴对称图形，它的对称轴是___________________________．
3、等腰三角形的对称轴是_____，等边三角形有_____条对称轴，正方形有_____条对称轴，圆有_____条对称轴．
4、三角形三条角平分线的交点到_____距离相等．
*5、△ABC中，∠C=90°，AD平分∠BAC交BC于D，若BC=10，BD=6，则点D到AB的距离是_____．
二、选择题
6、下列图案中是轴对称图形的是（ ）
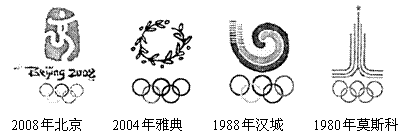
A、 B、 C、 D、
*7、将一张长与宽的比为2∶1的长方形纸片按如图①、②所示的方式对折，然后沿图③中的虚线裁剪，得到图④，最后将图④的纸片再展开铺平，则所得到的图案是（ ）
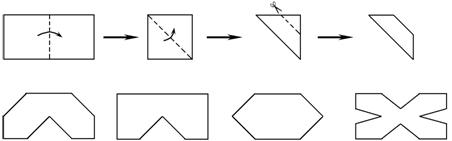
图① 图②
图③ 图④
A、 B、 C、 D、
8、下列几何图形中，一定是轴对称图形的有 （ ）
A、 2个 B、 3个 C、 4个 D、 5个
9、下列轴对称图形中，对称轴的条数最少的图形是（ ）
A、圆 B、正六边形 C、正方形 D、等边三角形
10、下列轴对称图形中，对称轴条数最少的是（ ）
A、等边三角形 B、正方形 C、正六边形 D、圆
11、下列图形中对称轴最多的是（ ）
A、圆 B、菱形 C、正三角形 D、正方形
12、观察下列四个图案，其中为轴对称图形的是（ ）．
A、 B、 C、 D、
13、下列文字图案中，是轴对称图形的是（ ）
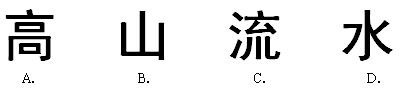
*14、三角形内有一点，这点到三角形三个顶点的距离都相等，则这点一定是三角形的（ ）
A、三边中垂线的交点 B、三条中线的交点
C、三条高的交点
D、三内角平分线的交点
15、下列图形中，轴对称图形的个数有（ ）
A、4个 B、3个 C、2个 D、1个
三、解答题
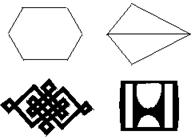
16、画出下列每个轴对称图形的对称轴
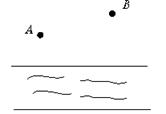
17、如图，在一条河的同岸有两个村庄A、B，两村要在河上合修一座桥到对岸去，桥修在什么地方，可以使两个村庄到桥的距离相等？
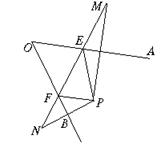
*18、如图，点P在∠AOB内，点M、N分别是点P关于OA、OB的对称点，若△PEF的周长为
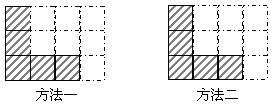
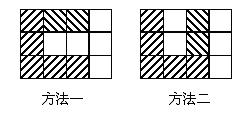
**19、如图，阴影部分是由5个小正方形组成的一个直角图形，请用二种方法分别在下图方格内添涂黑二个小正方形，使它们成为轴对称图形．
20、如图，已知
及两边上各一点
．求作一点
，使它到两点的距离相等，并且到两边的距离也相等．
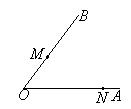
【试题答案】
一、1、它本身所在直线和它的垂直平分线
2、角平分线所在的直线
3、底边上的高所在直线 三 四 无数
4、三边的
5、4
二、DABDA ABBAB
三、16、略 17、略 18、20 cm
19、 解：此题答案不唯一，只要在方格内添的二个正方形使整个图形是对称图形就给分，每答对一个给4分，共8分．
20、略