【本讲教育信息】

一、教学内容：

空间几何体

二、学习目标

1、理解棱柱有关概念，掌握棱柱的性质，正棱柱的性质，灵活地进行位置关系的判断与论证，进而达到计算的目的。

2、了解棱锥的概念，正棱锥的有关性质，重点是与棱锥有关的问题。难点是两个重要的直角三角形的作用及平行截面性质的灵活应用。

3、了解球、球面的概念， 掌握球的性质及球的表面积、体积公式，理解球面上两点间距离的概念，了解球的内接、外切等几何问题的解法.

4、球面与球体的有关概念、性质与计算公式是重点，球面上两点间的距离是难点。

三、知识要点

1、若干个平面多边形围成的几何体，叫做多面体.

2、把多面体的任何一个面伸展为平面，如果所有其他各面都在这个平面的同侧，这样的多面体叫做凸多面体.

3、棱柱：

（1）棱柱的定义：有两个面互相平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，由这些面所围成的几何体叫做棱柱。

（2）棱柱的性质：①侧棱都相等，侧面都是平行四边形；②两个底面与平行于底面的截面是全等的多边形；③过不相邻的两条侧棱的截面是平行四边形。

（3）棱柱的分类：

按底面多边形的边数分类：三棱柱，四棱柱，…，n棱柱.

按侧棱与底面的位置关系分类：棱柱

（4）特殊的四棱柱:四棱柱平行六面体直平行六面体长方体正四棱柱正方体

（5）长方体对角线定理:长方体一条对角线的平方等于一个顶点上三条棱的长的平方和.

（6）棱柱公式: ，c是底面多边形的周长，h是直棱柱的高

，是棱柱的底面积，是棱柱的高.

（7）思维方式：割补法是求体积的基本方法，在体积的计算中常用到“等积变换”的技巧。

4、棱锥：

（1）定义：有一个面是多边形，其余各面是有一个公共顶点的三角形，由这些面所围成的几何体叫棱锥。

如果一个棱锥的底面是正多边形，并且顶点在底面的射影是底面中心，这样的棱锥叫做正棱锥。

（2）性质

Ⅰ、正棱锥的性质

①各侧棱相等，各侧面都是全等的等腰三角形。

②棱锥的高、斜高和斜高在底面上的射影组成一个直角三角形；棱锥的高、侧棱和侧棱在底面上的射影也组成一个直角三角形。

Ⅱ、一般棱锥的性质

定理 如果棱锥被平行于棱锥底面的平面所截，那么截面和底面相似，并且它们面积的比等于截得的棱锥的高和已知棱锥的高的平方的比。

（3）棱锥的公式：，a为底面边长，c 为底面周长，h 为斜高。

V=Sh，其中S是棱锥的底面积，h是高。

特别注意：在棱锥中，有两个截面（严格地说，是截面的一部分）值得注意：一个是由棱锥的侧棱和棱锥的高构成的直角三角形，另一个是由棱锥的斜高和棱锥的高构成的直角三角形，这两个直角三角形把棱锥的侧棱，侧棱与底面所组成的角、高、斜高，侧面与底面所成角都集中在同一个平面，有效地实现了立体问题向平面问题的转化。所以这两个“截面”（直角三角形）是解棱锥问题的“钥匙”。

5、棱台：棱锥被平行于底面的平面所截，截面和底面间的部分叫做棱台。

棱台的公式：，a为棱台上底面边长，c为上底面周长，为棱台下底面边长，为下底面周长，h为斜高。

，，h是台体的高。

6、圆柱、圆锥和圆台可以分别看作以矩形的一边，直角三角形的一直角边、直角梯形中垂直于底边的腰所在的直线为旋转轴，将矩形、直角三角形、直角梯形分别旋转一周而形成的曲面所围成的几何体。

7、球：

（1）球的概念：半圆以它的直径为旋转轴，旋转所成的曲面叫做球面。球面所围成的几何体叫做球。半圆的圆心叫做球心。连接球心与球上任意一点的线段叫做球的半径。连接球面上两点并且经过球心的线段叫做球的直径。球面被经过球心的平面所截得的圆叫做大圆。被不经过球心的截面截得的圆叫做小圆。

（2）球的截面圆的性质：

①球心到截面圆心的连线垂直于截面；

②球心到截面的距离d与球的半径R及截面的半径r，有下面的关系：

r²=R²－d²。

（3）两点的球面距离的定义：在球面大圆上两点间的劣弧的长度。

求两点的球面距离的方法：将A、B两点与球心O连线，先求出弦长AB，在三角形ABO中求出∠AOB的弧度数，由弧长公式l=θR得到。

（4）球的表面积与体积：S_球面=4πR²，V=πR³。

【典型例题】

例1、（1）下列命题：①有一个侧面是矩形的棱柱是直棱柱；

②有两个侧面是矩形的棱柱是直棱柱；

③有两个相邻侧面是矩形的棱柱是直棱柱；

④有三个侧面是矩形的棱柱是直棱柱。

其中正确命题的个数是_______

A. 1 B. 2 C. 3 D. 4

分析：①②显然不对.③相邻两侧面的公共边即侧棱垂直于底面.④中侧棱也垂直于底面.故选B.

（2）若一个正棱锥的底面边长与侧棱长相等，则这个棱锥一定不是（ ）

A. 三棱锥 B. 四棱锥 C. 五棱锥 D. 六棱锥

解析：选D。若满足条件的正棱锥是六棱锥，则它的六个侧面都是正三角形，侧面的顶角都是60°，其和为360°，则顶点在底面内，与棱锥的定义相矛盾。

例2、三个平面可能把空间分成几部分？试画出可能的图形。

解：如下图所示

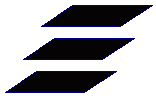
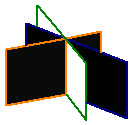
4部分 6部分 6部分

7部分 8部分

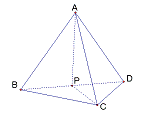
例3、求棱长为1的正四面体的体积。

方法1：利用棱锥的体积公式直接求证四面体的体积；

方法2：把正四面体分解为两个易求体积的小三棱锥，然后相加得到正四面体的体积，计算过程相对简单.

取BD的中点P，连接AP，CP，易证 BD面PAC，于是

因为等腰的三边易求，所以，正四面体的体积易求.

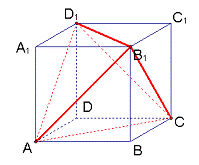
方法3：将正四面体置于某个正方体之中，把正方体看作整体，则四面体是正方体的一部分，如图：设正方体的棱长为，则所以正方体的棱长为，那么正四面体的体积就等于正方体的体积减去四个侧棱长为的小三棱锥的体积.

答案：

思维点拨：割补法是求体积常用的方法。

例4、已知平面及以下三个几何体：

（1）长、宽、高都不相等的长方体；

（2）底面为平行四边形，但不是棱形和矩形的四棱锥；

（3）正四面体.

问：这三个几何体在平面上的射影可以为正方形吗？

分析：此题如果把这三个几何体直接投影到平面上，再判断所得射影是正方形是很困难的.

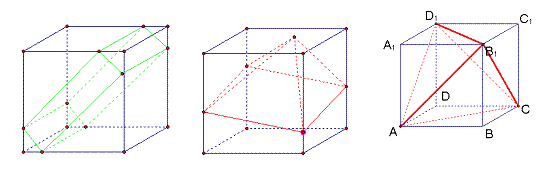
如上图所示构造正方体的内接长方体，四棱锥和正四面体，易知它们在正方体的底面射影都是正方形.

例5、在球内有相距9cm的两个平行截面，面积分别为49πcm²、400πcm²，则球的表面积为__________。

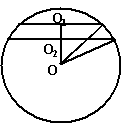
解：作球的一个大圆O，当两个截面在球心O的同侧时，解得R=25。当两个截面在球心O的两侧时无解。

∴S_球面=2500πcm²。

思维点拨：立体几何中的相互位置关系，也应注意分类讨论。

本讲涉及的主要数学思想方法

1、在解正棱锥问题时要注意利用四个直角三角形

2、四面体（即三棱锥）是最简单的棱锥，它的每一个面都可作棱锥的底面，它的每个顶点都可以作棱锥的锥顶，但无论如何转换底面和锥顶，棱锥的体积不变，这正是求点到面的距离的“体积法”的理论依据。

3、球的面积、体积及基本性质是解决有关问题的重要依据，它的轴截面图形、球半径、截面圆半径、圆心距所构成的直角三角形是把空间问题转化为平面问题的主要方法。

4、要正确区分球面上两点间的直线距离与球面距离；计算A，B两点的球面距离的关键是搞清纬度、经度、纬度差、经度差等概念。

具体步骤是：（1）计算线段AB的长度；（2）计算A、B到球心O的张角；（3）计算球的大圆在A、B两点间所夹的劣弧长。

5、注意平面几何知识在立体几何中的应用，以及将立体几何问题“平面化”即“降维”。计算问题必须要有严格的论证作为基础，不能只重计算结果，而轻视推理过程。

【模拟试题】（答题时间：60分钟）

一、选择题

1、设有四个命题：

①底面是矩形的平行六面体是长方体

②棱长相等的直四棱柱是正方体

③有两条侧棱都垂直于底面一边的平行六面体是直六面体

④体对角线相等的平行六面体是直平行六面体

以上四个命题中，真命题的个数是（ ）

A、1 B、2 C、3 D、4

2、下列命题

①有一个侧面是矩形的棱柱是直棱柱；

②有两个侧面是矩形的棱柱是直棱柱；

③有两个相邻侧面是矩形的棱柱是直棱柱；

④有三个侧面是矩形的棱柱是直棱柱。

其中正确命题的个数是（ ）

A、1 B、2 C、3 D、4

**3、棱长为1的正方体的8个顶点都在球的表面上，分别是棱，的中点，则直线被球截得的线段长为（ ）

A、 B、 C、 D、

4、有下列命题：

①过球面上任意两点只能作球的一个大圆；

②球的任意两个大圆的交点的连结是球的直径；

③用不过球心的截面截球，球心和截面圆心的连线垂直于截面；

④球是与定点的距离等于定长的所有点的集合；

⑤球面积是它大圆面积的4倍；

⑥球面上两点的球面距离，是这两点所在截面上以这两点为端点的劣弧的长

其中正确命题的个数是（ ）

A、2 B、3 C、4 D、5

5、“”是“直线平行于直线”的（ ）

A、充分而不必要条件 B、必要而不充分条件

C、充分必要条件 D、既不充分也不必要条件

*6、平面外有两条直线和，如果和在平面内的射影分别是和，给出下列四个命题：

①⊥⊥； ②⊥⊥；

③与相交与相交或重合； ④与平行与平行或重合；

其中不正确的命题个数是（ ）

A、1 B、2 C、3 D、4

二、填空题

7、一个长方体的各顶点均在同一球的球面上，且一个顶点上的三条棱的长分别为1，2，3，则此球的表面积为　　　　

**8、一个正三棱锥的四个顶点都在半径为1的球面上，其中底面的三个顶点在该球的一个大圆上，则该正三棱锥的体积是　　　　

*9、已知某个几何体的三视图如下，根据图中标出的尺寸（单位：cm），可得这个几何体的体积是　　　　

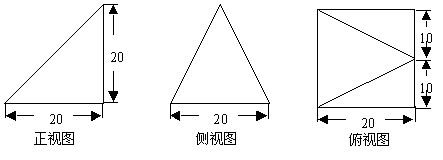
三、解答题

*10、已知过球面上三点A、B、C的截面到球心的距离等于球半径的一半，且AC=BC=6，AB=4，求球面面积与球的体积。

11、一个正四棱柱的各个顶点在一个直径为2cm的球面上。如果正四棱柱的底面边长为1cm，求该棱柱的表面积。

**12、把地球当作半径为R的球，地球上A、B两点都在北纬的纬线上，A、B两点的球面距离是，A在东经，求B点的位置。

【试题答案】

1、A 2、B 3、D 4、B 5、C 6、D 7、 8、 9、

10、解：设球心为O，球半径为R，

作OO₁平面ABC于O₁，由于OA=OB=OC=R，

则O₁是的外心，设M是AB的中点，

由于AC=BC，则O₁，设O₁M=x，

易知O₁MAB，则

，解得，则

O₁A=O₁B=O₁C=

在中，，，OA=R，由勾股定理得

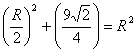，解得

故，

11、cm²。

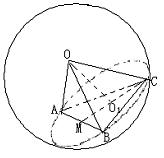
12、解：如图，求B点的位置即求B点的经度，

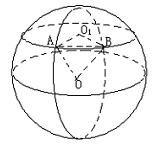
设B点在东经或西经

因为A、B两点的球面距离是，

因而三角形AOB是等边三角形，

又

求出，则或

所以，B点在北纬，东经或西经。