![]()
【本讲教育信息】
一. 教学内容:
展开与折叠、长方体的表面积
(一)展开与折叠
教学目标:
1. 通过动手操作,知道长方体、正方体的展开图,加深对长方体、正方体的认识
2. 在想象、操作等活动中,发展空间观念,激发学习数学的兴趣。
3. 了解长方体、正方体展开图的特点。
教学重点:
了解长方体、正方体展开图的特点。
教学难点:
在想象、操作等活动中,发展空间观念,激发学习数学的兴趣。
教学过程:
一、上周知识回顾
长方体和正方体的特征:
|
|
顶点 |
面 |
棱 |
|||
|
个数 |
个数 |
形状 |
大小关系 |
条数 |
长度关系 |
|
|
长方体 |
8 |
6 |
长方形(有时有2个相对的面为正方形) |
相对的面面积相等 |
12 |
可以分为3组,每组棱的长度相等 |
|
正方体 |
8 |
6 |
每个面都是正方形 |
6个面的面积都相等 |
12 |
所有的棱都相等 |
二、本周知识要点
(一)长方体和正方体展开图的特点
把一个长方体或正方体沿棱剪开,就会得到它的展开图,由于剪的方法不同,所以得到的展开图的形状也不相等。但无论形状怎样不同,展开图都具有长方体或正方体6个面的特点,像长方体展开图,它都是由6个小长方形组成的,相对面的面积两两相等,而且相邻的两个面一般面积不相等(特殊情况也有4个相邻的面面积相等的)。
正方体展开图是由6个小正方形组成的,而且6个小正方形的面积相等。
(二)判断哪些图形折叠后能围成长方体或正方体的方法
判断时,首先要依据长方体和正方体展开图的特点来进行判断,不符合长方体或正方体展开图特点的,肯定不能围成长方体或正方体,但不是所有符合特点的都可以围成长方体或正方体,在符合基本条件的基础上,还需要进一步判断,判断的方法有两种:
一种是实际动手操作,动手叠一叠,看能否围成长方体或正方体。
一种是运用空间想象,在脑海中想象图形折叠后的样子,判断能否围成长方体或正方体。
例题1. 下面哪些图形沿虚线折叠后能围成长方体?
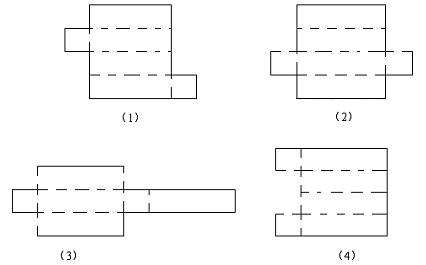
分析:根据长方体面的特征就能够判断出是否能围成一个长方体。长方体有六个面,每个面都是长方形也有可能有一组相对的面为正方形,相对的面形状相同面积相等。而本题中的这些长方体很明显都是那种特殊的长方体,就是有一组相对的面为正方形,其余的四个面是面积、形状相等的长方形。
解答:(1)(2)(3)都可以围成长方体,因为它们符合长方体的特点。而(4)就不行了,因为它的两个正方形的面,折叠后不能相对。
例题2. 如图,这是一个正方体纸盒的平面展开图,那么正方体中相对面的颜色各是什么?

分析:在做这道题时,我们可以通过空间想象,把这个展开图折叠成一个正方体,我们会发现如果“紫”是底面,那么“红”就是上面,“蓝”就是左面,“黄”面就是右面,“绿”就是前面,“白”就是后面。
解答:这个正方体中相对面颜色:紫对红、蓝对黄、绿对白。
(三)点燃你的思维
1. 下图是一个正方体的展开图,其中与3号面相对的是( )号面。开动脑筋,想一想。
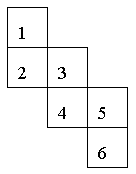
分析:这道题我们可以利用我们的空间想象和排除法解决。从正方体的特征中,我们清晰地知道,有公共棱的两个面是绝对不相对的,所以与3相对的面就可以将2、4两个面排除;有公共顶点的三个面也是绝对不相对的,所以与3相对的面就可以将1、5两个面排除。从而我们得到与3相对的面是6号面。用这个方法同时也能快速地判断出其它面相对的情况。
解答:与3号面相对的面是6号面。
2. 一个正方体木块的棱长是3厘米,表面涂满油漆,把它切成棱长为1厘米的小正方体若干块。在这些小正方体中,三面涂有红漆的有多少块?两面涂有红漆的有多少块?一面涂有红漆的有多少块?
分析:三面涂有红漆的,只能是八个角的小正方体,所以有8块;两面涂有红漆的,是每个边的中间1块,所以有12块;而一面涂有红漆的,则是每个面中最中心的一块,所以有6块。
解答:三面涂有红漆的有8块;两面涂有红漆的有12块;一面涂有红漆的有6块。
(二)长方体的表面积
教学目标:
1. 在操作、观察活动中,探索并理解长方体、正方体的表面积及其计算方法,并能正确计算。
2. 丰富对现实空间的认识,发展初步的空间观念。
3. 结合具体情境,解决活动中一些简单的问题,体会数学与生活的联系。
教学重点:
在操作、观察活动中,探索并理解长方体、正方体的表面积及其计算方法,并能正确计算。
教学难点:
丰富对现实空间的认识,发展初步的空间观念。
一、旧知识回顾
长方形面积的计算方法:长方形面积=长×宽
正方形面积的计算方法:正方形面积=边长×边长
二、本周知识要点
(一)长方体和正方体表面积的意义
长方体或正方体6个面的面积之和,叫做它们的表面积。
(二)不同长方体表面积的不同求法
1. 一般的长方体(即长、宽、高都不相等的长方体)。
根据长方体的长、宽、高,可以确定每个面的长和宽,根据“长方形面积=长×宽”,我们可以知道:“前面的面积=后面的面积=长×高”,“左面的面积=右面的面积=宽×高”,“上面的面积=下面的面积=长×宽”。
长方体的表面积=(长×宽+长×高+宽×高)×2
例题:一个长方体,长是5厘米,宽是7厘米,高是6厘米,这个长方体的表面积是多少平方厘米?
(5×7+5×6+7×6)×2=214(平方厘米)
答:这个长方体的表面积是214平方厘米。
2. 特殊的长方体(比如上面和下面是相同的正方形的长方体)。
除这组相对的面为正方形的面,其余的四个面为面积、形状相同的长方形。
长方体的表面积=长×宽×2+长×高×4
例题:一个长方体,长是7厘米,宽是7厘米,高是10厘米,这个长方体的表面积是多少平方厘米?
7×7×2+7×10×4=378(平方厘米)
答:这个长方体的表面积是378平方厘米。
(三)正方体表面积的求法
因为正方体6个面的面积都相等,而一个面的面积等于“棱长×棱长”,所以正方体表面积公式是:
正方体表面积=棱长×棱长×6
例题:给棱长为0.8米的正方体木箱的表面涂上油漆,涂油漆部分的总面积是多少?
0.8×0.8×6=3.84(平方米)
答:涂油漆部分的总面积是3.84平方米。
(四)根据实际情况求长方体或正方体的表面积
在实际生产和生活中,根据实际需要,在计算长方体和正方体的表面积时,有时不需要计算6个面的面积和。例如:无盖的长方体水桶,我们就不需要计算上面的面积;涂屋子中的一根长方体柱子,一般只需计算它的前、后、左、右四个面的面积即可。
三、点燃你的思维
1. 把4个完全一样的正方体一字排开,拼成一个长方体,它的表面积是360平方厘米,求原来一个正方体的表面积。
分析:4个正方体有24个面,因为拼成长方体,要减少6个面,所以长方体的表面积是18个面的总面积,可以 求出一个面的面积,然后再求出正方体6个面的面积,即一个正方体的表面积。
解答:6×4-6=18
360÷18=20(平方厘米)
20×6=120(平方厘米)
答:原来一个正方体的表面积是120平方厘米。
归纳:n个正方体一字排开,拼成长方体,减少的面积是(n-1)×2个正方形的面积。
2. 一种长方体木块,长、宽、高分别是5厘米、3厘米、2厘米,用2个这样的木块拼成的长方体,表面积最大是多少平方厘米?
分析:要想表面积最大,就必须把最小的面拼接在一起,用两个长方体的表面积之和减去拼接的两个面,则可求出新的长方体的表面积。
解答:(5×3+5×2+2×3)×2×2-2×3×2=112(平方厘米)
答:表面积最大是112平方厘米。
归纳:几个完全一样的长方体,拼成一个更大的长方体,要想使表面积最大,必须把最小的面拼接在一起,要想使表面积最小,必须把最大的面拼接在一起。
【模拟试题】(答题时间:25分钟)
1、判断下列图形能否折叠成正方体。在能折叠成的图形下面画“√”。
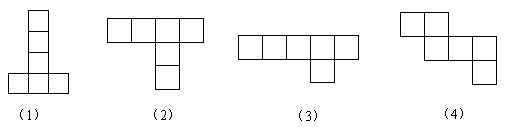
2、先观察,再连线。
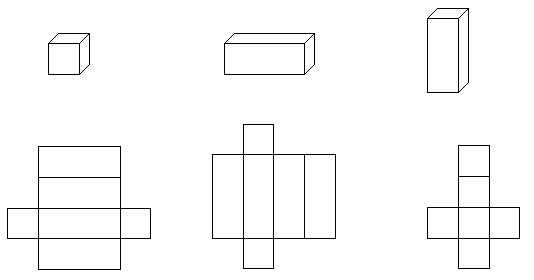
3、填一填
(1)一个长方体的长是8厘米,宽是6厘米,高是4厘米,它的表面积是( )平方厘米,棱长和是( )厘米。
(2)一个正方体的棱长是8厘米,它的表面积是( )平方厘米,它的棱长和是( )厘米。
(3)19平方厘米=( )平方分米
70平方米=( )平方分米
0.91平方米=( )平方厘米
1.25平方米=( )平方米( )平方厘米
4、我做小法官。
(1)长方体的展开图折叠后不一定就能围成长方体。( )
(2)长方体的展开图一定是由六个长方形组成的,不能有正方形。( )
(3)正方体的展开图是由六个正方形组成的。( )
(4)只要是由六个完全一样的正方形组成的图形就一定能折叠成正方体。( )
(5)正方体棱长扩大3倍,表面积扩大9倍。( )
(6)正方体棱长扩大3倍,棱长和扩大3倍。( )
(7)一个正方体的棱长是4分米,它的占地面积是48平方分米。( )
(8)一个正方体的占地面积就是它的表面积。( )
5、一种无盖的长方体水桶,长是5分米,宽是4分米,高是8分米,做这样一对水桶,至少需要铁皮多少平方分米?(接口处忽略不计)
6、用48厘米的铁丝折成一个正方体框架,这个正方体的表面积是多少?
![]()
【试题答案】
1、判断下列图形能否折叠成正方体。在能折叠成的图形下面画“√”。
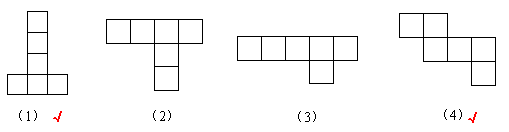
2、先观察,再连线。
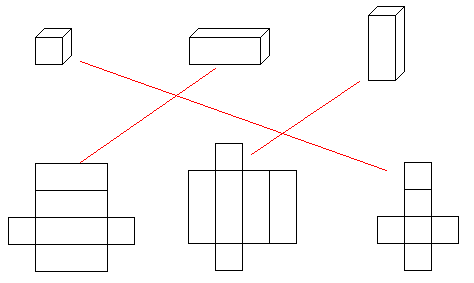
3、填一填
(1)一个长方体的长是8厘米,宽是6厘米,高是4厘米,它的表面积是(208)平方厘米,棱长和是(72)厘米。
(2)一个正方体的棱长是8厘米,它的表面积是(384)平方厘米,它的棱长和是(96)厘米。
(3)19平方厘米=(0.19)平方分米
70平方米=(7000)平方分米
0.91平方米=(9100)平方厘米
1.25平方米=(1)平方米(2500)平方厘米
4、我做小法官。
(1)长方体的展开图折叠后不一定就能围成长方体。(×)
(2)长方体的展开图一定是由六个长方形组成的,不能有正方形。(×)
(3)正方体的展开图是由六个正方形组成的。(√)
(4)只要是由六个完全一样的正方形组成的图形就一定能折叠成正方体。(×)
(5)正方体棱长扩大3倍,表面积扩大9倍。(√)
(6)正方体棱长扩大3倍,棱长和扩大3倍。(√)
(7)一个正方体的棱长是4分米,它的占地面积是48平方分米。(×)
(8)一个正方体的占地面积就是它的表面积。(×)
5、一种无盖的长方体水桶,长是5分米,宽是4分米,高是8分米,做这样一对水桶,至少需要铁皮多少平方分米?(接口处忽略不计)
(5×4+5×8+4×8)×2=184(平方分米)
184-5×4=164(平方分米)
164×2=328(平方分米)
答:至少需要铁皮328平方分米。
6、用48厘米的铁丝折成一个正方体框架,这个正方体的表面积是多少?
48÷12=4(厘米)
4×4×6=96(平方厘米)
答:这个正方体的表面积是96平方厘米。