【本讲教育信息】
一. 教学内容：
第一章 第4节 斜抛运动
二. 教学知识点：
知识点1 斜抛运动及其特点
1、斜抛运动的概念及特点
将物体以一定的初速度斜向上方抛出后，物体所做的运动叫做斜抛运动。
做斜抛运动的物体，在忽略空气阻力的情况下由于只受重力的作用，因此，斜抛运动是匀变速曲线运动。
轨迹特点：做斜抛运动的物体，先是沿着曲线上升，到达最高点后，又沿着曲线下降。图1中的曲线OAB就是斜抛物体的运动轨迹。
图1
2、斜抛运动的研究方法
利用运动的合成与分解。
由于斜抛运动在不考虑空气阻力的情况下，只受重力作用，因此，对斜抛运动也有多种分解方法。
方法一：类似于研究平抛运动，我们以抛出点为坐标原点，建立直角坐标系，把初速度分解为沿水平方向的分量
和竖直方向的分量
，这样，就可以将斜抛运动分解为水平方向上的匀速直线运动和竖直向上的匀减速直线运动，如图2所示。
图2
方法二：分解为沿初速度方向的匀速直线运动和竖直方向的自由落体运动。如图3所示，每经过1s物体沿初速度方向走过相等的距离；而在竖直方向上，物体按自由落体运动的规律，在1s内、2s内、3s内……的下落距离之比为1：4：9……
根据以上分析，我们可以画出物体做斜抛运动时的轨迹（如图3所示）
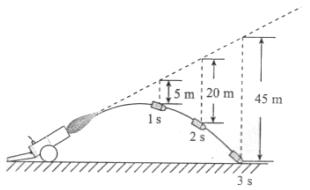
图3
知识点2 斜抛运动的规律
如图4所示，为质点初速度为
，倾角为
的斜抛运动的示意图。
图4
1、速度公式
水平速度
；
竖直速度
。
2、位移公式
水平位移
；
竖直位移
；
由上两式可得
这就是斜抛物体的轨迹方程。
3、斜抛运动的射程和射高
射程是做斜抛运动物体的水平位移，射高是做斜抛运动物体上升的最大高度。
飞行时间t：
；
射高h：
；
射程s：
由此可见，在给定的情况下，当
时，射程最大，
。
三. 易错点透析
（1）注意斜抛的对称性。
（2）对速度进行分解时要注意。一般沿竖直方向与水平方向分解。
例：如图5所示，斜上抛，分解成竖直方向上的竖直上抛运动与水平方向的匀速直线运动。
图5 图6
如图6所示，斜下抛，可分解成竖直方向上的竖直下抛运动与水平方向的匀速直线运动。
这样便于用已学知识找出斜抛运动的规律。
抛体理论在体育运动中的应用
抛体运动理论在体育运动中可以用来描述初速度、初始角度以及初始高度对运动成绩的影响，并寻找它们之间的最佳组合，因此抛体运动理论在体育中有重要意义。
（1）斜抛运动的基本规律
在忽略空气阻力和物体自转引起的影响时，运动是二维的，如图7所示，设初速度为，初始角度为
，根据斜抛运动规律可得
图7
水平速度
，
竖直速度
。
射程
，
射高
（2）滑步推铅球落地点比出手点低△h，将
代入方程
和方程，可得
，
联立可解得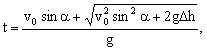
由此可见，影响投掷距离的因素有初速度，初始角度为
和抛出点与落地点的高度差△h，增加初速度是提高成绩的关键，增加出手高度、选取合适的出手角度也能提高投掷成绩。
【典型例题】
一、用运动合成与分解的方法来讨论斜抛运动
例1. 以相同的初速度，不同的抛射角同时抛出三个小球A、B、C，A、B、C三球在空中的运动轨迹如图1所示，下列说法中正确的是（ ）
图1
A. A、B、C三球在运动过程中，加速度都相同
B. B球的射程最远，所以最迟落地
C. A球的射程最大，所以最迟落地
D. A、C两球的射程相等，两球的抛射角互为余角，即
解析：A、B、C三球在运动过程中，只受到重力作用，故具有相同的加速度g，A正确。斜上抛运动可以分成上升和下落两个过程，下落过程就是平抛运动，根据平抛物体在空中的时间只决定于抛出点的高度可知，A球从抛物线顶点落至地面所需的时间最长，再由对称性可知，斜上抛物体上升和下落所需的时间是相等的，所以A球最迟落地。已知A、C两球的射程相等，根据射程公式
可知
，在
的情况下，必有
，才能使等式成立，故D正确。
答案：AD
点拨：用运动的合成与分解的方法来讨论斜抛运动，理解斜抛运动的处理方法。
借题发挥1：在塔顶上分别以跟水平线成45°角斜向上的、水平的，跟水平线成45°角斜向下的三个方向开枪，子弹射到地面时的速度大小分别为
和
（设三种方向射出的子弹的初速度的大小都一样，不计空气阻力），那么（D）
A. 
B.
C. 
D.
例2. 如图2所示，从距离墙壁为l的水平地面上的A点，以初速度、抛射角，斜向上抛一球，球恰在上升到最高点时与墙相碰，碰后被水平反弹回来，落到地面上的C点，且OC＝1/2。则小球被反弹的速度
的大小与初速度的大小之比为（ ）
图2
A. 1：2 B.
C.
D.
解析：斜抛运动以其顶点为界，可以分成上升和下降两个过程，这两个过程有一定对称性。下降过程实际上就是以水平分速度
为初速度的平抛运动。如果小球上升到最高点与墙壁碰撞后速度大小不变，仍为，则小球碰撞后做平抛运动，轨迹形状与上升时相同，即从B到C，再把B到A的过程与B到C的过程相比较。它们从同一高度被水平抛出，因此，在空中飞行的时间t相等，根据水平位移之比
，可得反弹速度
，即
答案：D
点拨：物体以速度v斜向上（或斜向下）抛出，与水平方向的夹角为，则水平方向的速度
，竖直方向的初速度
。
①斜上抛运动分解为水平方向的匀速直线运动和竖直方向的竖直上抛运动：
②斜上抛运动还可分解为：沿初速度方向的匀速直线运动和竖直方向上的自由落体运动。
③斜下抛运动通常分解为：水平方向的匀速直线运动和竖直方向上的竖直下抛运动：
。
例3. 图3所示的是做斜抛运动的物体在几个位置时的速率。分析图中给出的速度，你找到了什么规律？
你能用理论分析的方法证明这一规律吗？
解析：由图3中所提供的物体在不同位置时的速度的大小可知，斜上抛运动的物体，在同一高度处的速率大小相等。
图3
证明：斜上抛运动的物体在水平方向做匀速直线运动，；在竖直方向做竖直上抛运动，，当物体运动到高度为h的位置时，物体的竖直速度分量
，由速度的合成法则知，此时物体的速率
（其中g和h都是矢量）。
可见，做斜抛运动的物体在高度h处的速率
，在初速度和重力加速度一定的情况下，v仅由高度h决定。故斜上抛运动的物体在同一高度处速率大小相等。
方法点拨：此题考查学生分析并获取有用信息的能力。例如本题提供出斜抛运动的物体在多个不同位置时的速率，其中有用的信息是：（1）随着高度的增大，物体的速率减小；（2）在同一高度处物体运动的速度大小相等，论证的过程要求明确物体的运动规律，理清论证的思路，简化论证的过程，这也是一种必备的能力。
例4. 如图4所示，一架飞机距地面的高度为h，以匀速
水平飞行。今有一高射炮要击中飞机，设高射炮炮弹的初速度为，与水平方向的夹角为，并设发射时飞机在高射炮的正上方，空气的阻力可不计，那么要击中飞机，必须满足什么条件？并讨论和的关系。
解析：炮弹击中飞机必须满足的第一个条件
即在同一时刻炮弹和飞机的横坐标相等。
炮弹击中飞机的第二个条件是飞行的最大高度
。
由两个条件得
所以
所以，击中条件是
和
不同，就不同，但是整体要满足上面两个推论结果。
方法点拨：画出运动示意图，明确相关物体的运动位移和速度的关系，寻找相关的几何关系，是解决这类问题的关键所在。
【模拟试题】（答题时间：40分钟）
1、关于做斜抛运动（不计空气阻力）的物体，下列说法中正确的是（ ）
A. 初速度越大，射程越大
B. 抛射角越大，射程越小
C. 初速度一定时，抛射角越大，射程越小
D. 抛射角一定时，初速度越大，射程越大
2、A、B两物体初速度相同，A沿与水平方向成角的光滑斜面上滑；B与水平方向成角斜上抛。它们所能达到的最大高度分别为
和
，则（ ）
A. 
B.
C. 
D.
无法确定
3、做斜上抛运动的物体（ ）
A. 水平分速度不变
B. 加速度不变
C. 在相同的高度处有相同的速度
D. 经过最高点时，瞬时速度为零
4、如图1所示，已知炮弹的初速度是
，今把大炮置于高度为
图1
（1）发射时炮筒的仰角；
（2）炮弹落地时的速度（g取
）
5、一个棒球以
（1）该球的飞行时间；
（2）该球上升达到的最大高度；
（3）射程。（g取
）
6、斜向上抛一球，抛射角
，当
时，球仍斜向上上升，但方向已跟水平成
角。求：
（1）球的初速度是多少？
（2）球将在什么时候达到最高点？（g取）
7、用60°的抛射角向天空发射焰火，若焰火引线的燃烧时间为6s，希望它在）
8、一足球运动员开出角球，球的初速度是
（1）落点与开出点之间的距离；
（2）球在运行过程中，球离地面的最大距离。（g取）
9、（2007·潍坊模拟）一座炮台置于距地面
（1）炮弹所达到的最大高度；
（2）炮弹落到地面时的时间和速度的大小；
（3）炮弹的水平射程。（忽略空气阻力，g取）
10、如图2所示，从A点以某一初速度抛出一个小球，在离A点水平距离为s处有一堵高度为h的墙BC，要求小球能越过B点。问小球以怎样的速度抛出，才能使小球恰好越过墙壁？
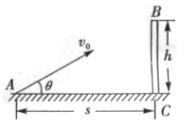
图2
【试题答案】
1、D
2、A
3、AB
4、（1）37°或（48.36°）
（2）
5、（1）
（2）
（3）
6、（1）
（2）
7、
8、（1）
（2）
9、（1）
（2）
（3）
10、